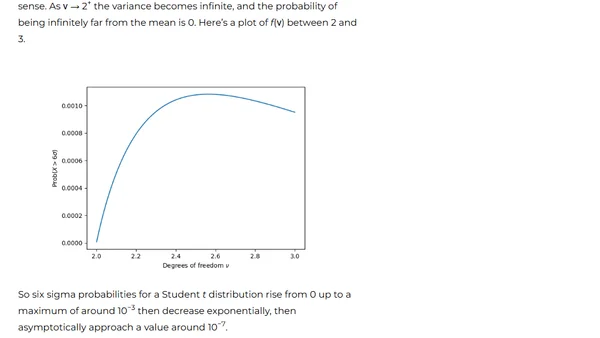
Explores the probability of extreme 'six sigma' events using the Student t distribution, showing it's not monotonic and depends heavily on degrees of freedom.
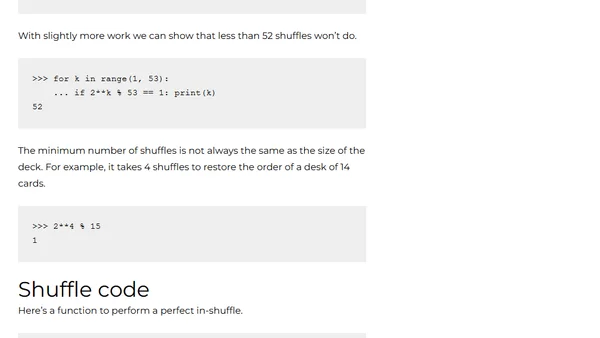
Explores the mathematics of card shuffling, contrasting random 'rifle shuffles' with deterministic 'perfect shuffles' and their Python implementation.
A machine learning professor critiques the foundational concept of a 'data-generating distribution' and shares insights from teaching a truly distribution-free course.
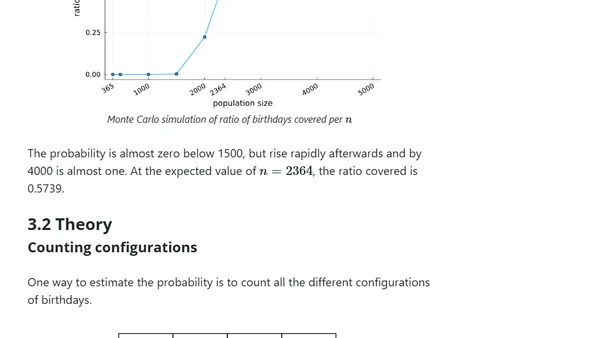
Analyzing the probability of covering all birthdays in a group and the expected number of people needed, framed as the Coupon Collector's Problem.
Using R simulations to calculate birthday probabilities instead of complex probability math, with code examples.
An update on the polymath research project about non-transitive dice and its statistical implications for the Wilcoxon/Mann-Whitney test.
Explains why pairwise independence of variables does not imply joint independence, using a chessboard as an intuitive counterexample.
A mathematical and computational exploration of the probability of a coin landing on its edge, inspired by Matt Parker's question about a 'three-sided coin'.
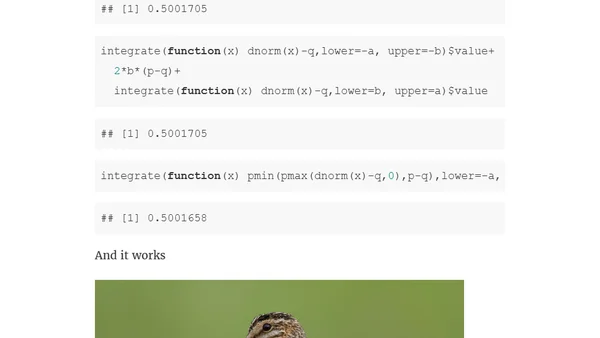
A technical analysis verifying a statistical calculation from an XKCD comic, involving normal distribution probabilities and R code.
A technical article discussing debugging tricks for complex statistical models with symmetries, focusing on verification and small-sample testing.
Explores methods for computing tail probabilities of linear combinations of chi-squared variables, focusing on applications in genetics with large datasets.
Analyzing the probability of self-assignment in a Secret Santa gift exchange using probability bounds and simulations.
A technical discussion on asymptotic approximations in stratified sampling when sampling probabilities approach zero, relevant for rare disease studies.
Explores a potential 'Polymath' project on the Wilcoxon test's non-transitive behavior with dice, connecting math and statistics.
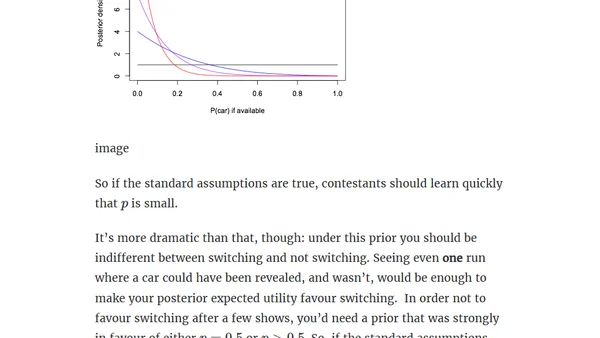
Analyzing the Monty Hall problem, exploring learning strategies and optimal decisions based on observed game history and host behavior.
Using R code to generate permutations of digits (2,2,5,5,9,9), analyzing divisibility by 11 and primality.
Analyzing a classic probability problem involving dice rolls, its historical context with Newton and Pepys, and the mathematical intuition behind it.
Explains how the birthday paradox applies to hash collisions, deriving the expected number of collisions in a set.
Explores non-transitivity in games like rock-paper-scissors, its history, and connections to statistics, evolution, and voting systems.
