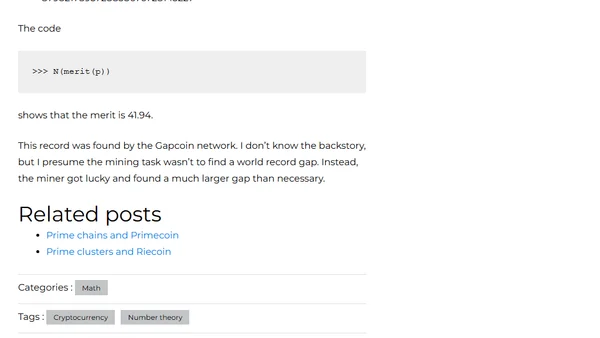
Explores prime gaps, their mathematical merit, and their use as proof-of-work in the Gapcoin cryptocurrency.
Explores prime clusters, their mathematical definition, and their use as proof-of-work in the Riecoin cryptocurrency.
Explores bi-twin prime chains, a mathematical pattern where sequences of twin primes follow a doubling rule, with examples and Python verification code.
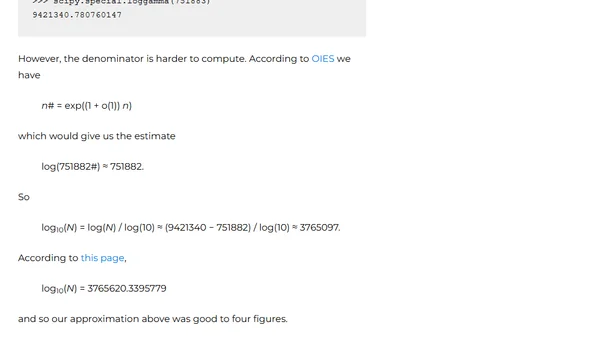
A new record for the largest known 'compositorial prime' has been set, a prime number with over 3.7 million digits.
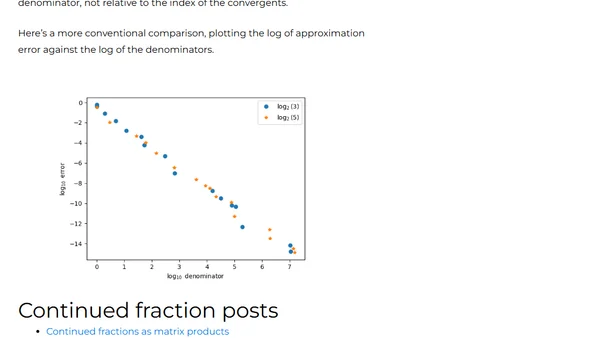
Analyzes the rational approximation of log2(3) and log2(5) using continued fractions, comparing their approximation errors.
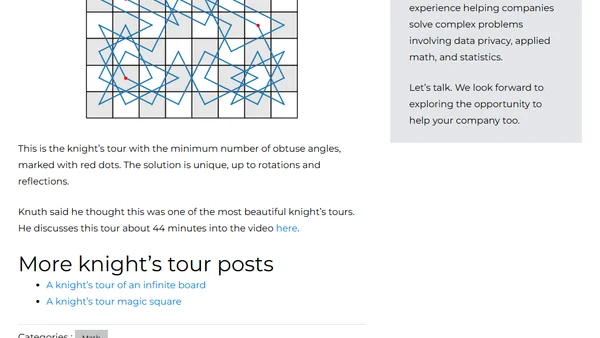
Analysis of a unique knight's tour with minimal obtuse angles, presented by Donald Knuth in his annual Christmas lecture.
Explores why category theory requires collections larger than sets to be interesting, discussing foundational issues and cardinality.
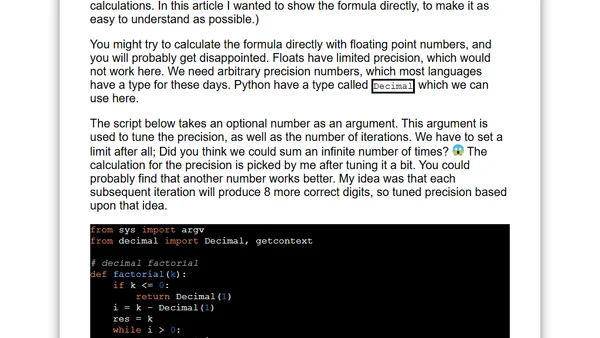
Celebrates Pi Day with two math tricks: a party trick using the 'Rule of 37' and a computer implementation of Ramanujan's formula for calculating Pi.
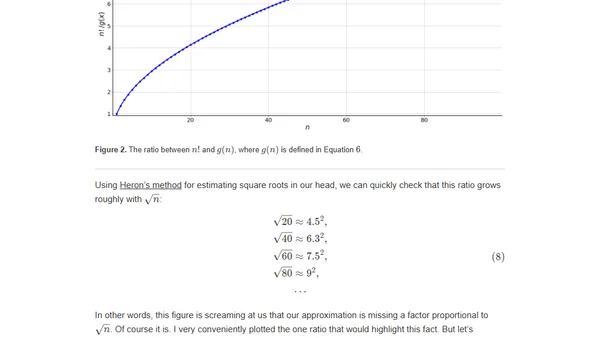
Explores the historical reasoning behind Stirling's approximation for factorials using basic calculus and intuitive mathematical approximations.
An update on the polymath research project about non-transitive dice and its statistical implications for the Wilcoxon/Mann-Whitney test.
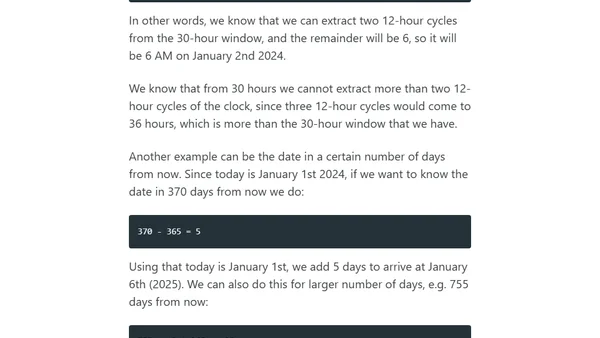
Explains the modulo operation using real-world examples like days of the week, clock time, and calendar dates.
Explores the potential and implications of using AI to automate mathematical theorem proving, framing it as a 'tame' problem solvable by machines.
Explores combinatory logic using bird metaphors, connecting the S and K combinators to lambda calculus and programming concepts.
Explains why pairwise independence of variables does not imply joint independence, using a chessboard as an intuitive counterexample.
A mathematical and computational exploration of the probability of a coin landing on its edge, inspired by Matt Parker's question about a 'three-sided coin'.
A deep dive into the Neural Tangent Kernel (NTK) theory, explaining the math behind why wide neural networks converge during gradient descent training.
A mathematical critique of additive scoring in grading and grant reviews, arguing for non-additive monotone functions.
A mathematical analysis of why a garden sprinkler waters unevenly, deriving equations for water distribution and proposing a technical fix.
Introduces linear algebra concepts like vector spaces and orthogonality as a foundation for understanding generalized Fourier series expansions.
Explores generalized Fourier series expansions using orthogonal function bases, with examples from Legendre polynomials and practical Jupyter notebook code.
