Explores categorical models for dependent type theory, connecting lambda calculus to fibrations and sections in locally cartesian closed categories.
Explores combinatory logic using bird metaphors, connecting the S and K combinators to lambda calculus and programming concepts.
Explores combinatory logic puzzles using bird metaphors, focusing on the self-fond Kestrel (K) and its logical properties.
Explores the connection between mockingbirds and fixpoints in combinatorial logic, using bird metaphors to discuss formal systems.
A technical introduction to combinatory logic using the metaphor of birds, based on the book 'To Mock a Mockingbird'.
Introduces the 'data exploration calculus', a theoretical model capturing the unique programming patterns used by data scientists and journalists for exploratory data analysis.
Exploring the untyped Lambda Calculus, Church numerals, and the Y Combinator by implementing them in Go's type system.
Explains how to execute Lambda Calculus, covering alpha-equivalence, beta-reduction, and normal forms in this practical guide.
An introduction to Lambda Calculus syntax, explaining its core concepts and expressions with practical JavaScript examples for programmers.
Explores whether mathematical concepts like lambda calculus are human inventions or universal truths, using philosophy of mathematics to frame the question.
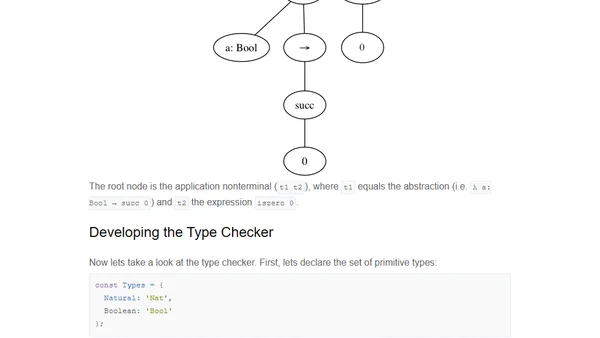
A guide to building a statically typed functional language, covering type checking, interpretation, and transpilation to JavaScript.
A thought experiment exploring how to build fundamental programming constructs like lists and numbers using only lambda calculus and closures in JavaScript.
