A detailed proof walkthrough of the De Moivre–Laplace theorem, the earliest version of the central limit theorem for the binomial distribution.
Discusses the practical choices in setting up asymptotic models for statistics, using examples from clinical trials and big data.
An introduction to Fisher Information, a statistical concept that quantifies how much information data samples contain about unknown distribution parameters.
Explains Chebyshev's inequality, a probability bound, and its application to calculating Upper Confidence Limits (UCL) in environmental monitoring.
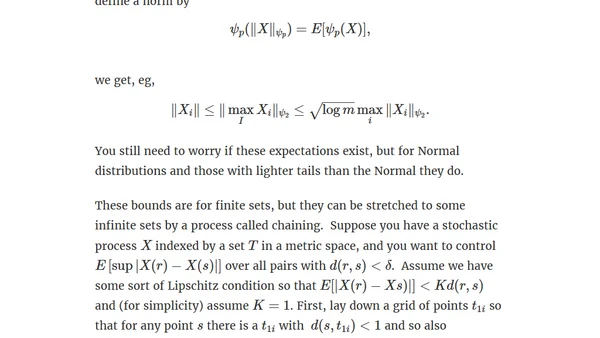
A mathematical exploration of bounds for the expected maximum of random variables, covering inequalities, norms, and chaining techniques for stochastic processes.
Explores Bayesian inference when data strongly contradicts prior expectations, analyzing how heavy-tailed priors and likelihoods affect posterior beliefs.
Explores various mathematical proofs for the Central Limit Theorem, comparing approaches like characteristic functions, the Lindeberg trick, entropy, and moments.
Explores different proofs of the Continuous Mapping Theorem in probability theory, discussing their merits and pedagogical value.
A philosophical and technical exploration of the practical meaning of measurability in mathematical statistics, questioning its necessity for real-world data analysis.
