Dan Simpson is a technical writer and researcher focusing on C++, JAX, and advanced statistical computing. His blog dives deep into sparse matrices, autodiff, Bayesian methods, and modern AI techniques, blending theory with practical, hands-on implementations.
18 articles from this blog
Explains how to compute specific entries of the inverse of a sparse symmetric positive definite matrix in C++ using Eigen and the Takahashi recursions.
A technical guide on building a block sparse matrix in C++ using the Eigen library, focusing on memory layout and performance.
A technical exploration of implementing Laplace approximations using JAX, focusing on sparse autodiff and JAXPR manipulation for efficient gradient computation.
A non-expert's humorous exploration of diffusion models as a method for sampling from arbitrary probability distributions, touching on measure transport.
Explores Markovian Gaussian Processes, focusing on theory and computational approximations to reduce memory and speed up linear algebra.
Exploring JAX-compatible sparse Cholesky decomposition, focusing on symbolic factorization and JAX's control flow challenges.
Explores the impact of using an incorrect acceptance probability in MCMC algorithms, discussing theory and literature on algorithm robustness.
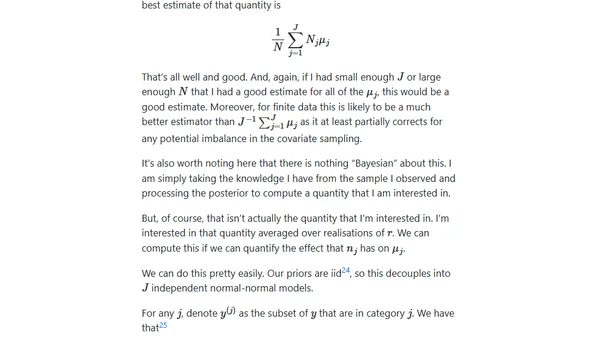
A deep dive into the Robins and Ritov statistical paradox, exploring a counterexample where subjective Bayesian inference fails and arguing for a resolution.
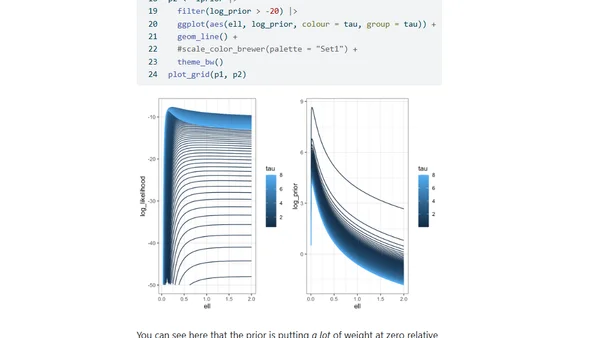
A technical guide exploring Penalised Complexity (PC) priors for Gaussian process parameters, including theory and derivation.
A technical blog post discussing penalized complexity priors in Bayesian statistics, focusing on how to set priors that appropriately penalize model complexity.
Explores the instability of importance sampling estimators and introduces truncated importance sampling (TIS) to stabilize variance by modifying large importance ratios.
Part 6 of a series on making sparse linear algebra differentiable in JAX, focusing on implementing Jacobian-vector products for custom primitives.
Part five of a series on implementing differentiable sparse linear algebra in JAX, focusing on registering new JAX-traceable primitives.
Explores design options for implementing autodifferentiable sparse matrices in JAX to accelerate statistical models, focusing on avoiding redundant computations.
Explores challenges integrating sparse Cholesky factorizations with JAX for faster statistical inference in PyMC.
Explores the Cholesky factorization algorithm for sparse matrices, detailing its mathematical derivation and computational considerations.
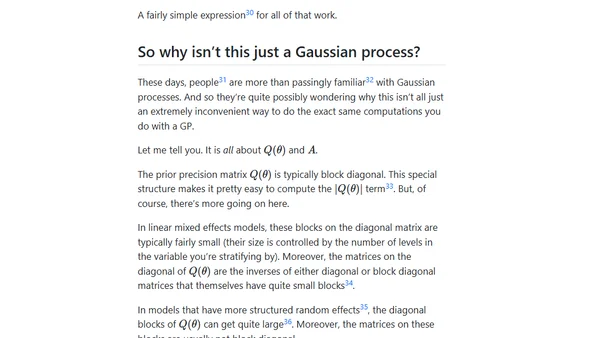
Explores using sparse linear algebra to speed up Bayesian inference for linear mixed models and generalizations, with a focus on Python/JAX prototyping.
A technical blog post discussing Bayesian priors, sparsity in high-dimensional models, and scale-mixture of normal priors for statistical computation.
