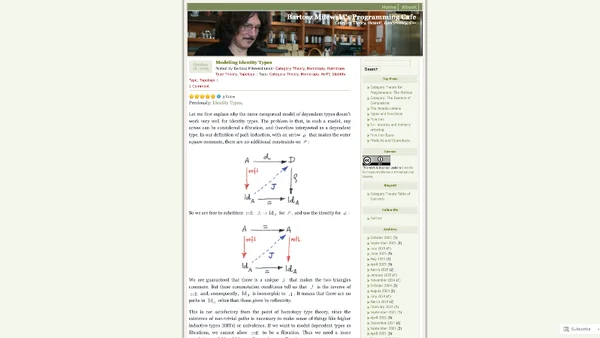
Modeling Identity Types
Explores advanced categorical modeling of identity types in homotopy type theory, focusing on fibrations, cofibrations, and path objects.
Bartosz Milewski is a programmer and former theoretical physicist known for bridging category theory and practical software development. He writes about Haskell, C++, concurrency, and functional programming, and is the author of Category Theory for Programmers.
7 articles from this blog

Explores advanced categorical modeling of identity types in homotopy type theory, focusing on fibrations, cofibrations, and path objects.
Explores identity and equality types in type theory, contrasting definitional vs. propositional equality and their role in proofs.
Explores categorical models for dependent type theory, connecting lambda calculus to fibrations and sections in locally cartesian closed categories.
Explores the concept of (weak) factorization systems in category theory, generalizing function decomposition into surjections and injections.
Explores the categorical definition of a subobject classifier, a key concept in topos theory, using set theory as a foundation.
A clear explanation of the attention mechanism in Large Language Models, focusing on how words derive meaning from context using vector embeddings.
A deep dive into composing comonads in Haskell, using Conway's Game of Life and Advent of Code puzzles to explore category theory and functional programming.